Synergy between electromagnetic and gravitational fluid dynamics

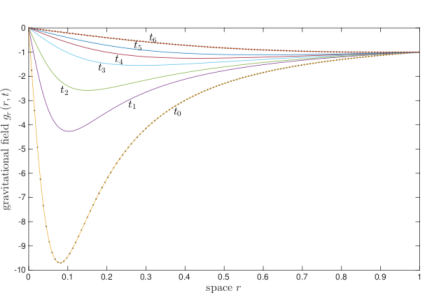
In several applications it is relevant to quantify the energy exchanges for a system embedded in an electromagnetic field, and to solve the typical equations of electromagnetic fluid dynamics. In order to model such systems, several approximations are usually adopted because of the diculty (in some cases, impossibility) to solve, even numerically, the electromagnetic fluid dynamics equations.It is then worth to move to a similar problem that can be handled and that can, in principle, allow to export the developed methodology into the electromagnetic case. In this context, gravitational fluid dynamics represents an interesting and useful test case, due to the possibility to express the basic equations in exactly the same formalism as the Maxwell equations, which describe the evolution in time and space of the electric and magnetic fields. Indeed, also in the case of the gravitational field, Maxwell-like equations can be derived. These equations allow to define two fields that describe the gravitational field and its evolution in time and space. The additional advantage of such an approach is the handy def- inition of the numerical constants that appear in the Maxwell-like equations and that are naturally provided by writing the gravitational field dynamics equations.Consistently with the goals of the present project, the solution of these equa- tions have been performed for the case study of a perfect gas enclosed in a spherical box placed in the interstellar space where all external forces are neg- ligible. Thus the gas is subject to only its own self-induced gravitational field, other than to thermal and viscous dissipation effects.